使用Python實現牛頓法迭代法

最近看到牛頓迭代法和二分法，現在用 python 實現一下

一、使用二分法實現開方#

假設求根號 5，二分法的基本思路是

a:折半： 5/2=2.5
b:平方校驗: 2.5*2.5=6.25>5，並且得到當前上限2.5
c:再次向下折半:2.5/2=1.25
d:平方校驗：1.25*1.25=1.5625<5,得到當前下限1.25
e:再次折半:2.5-(2.5-1.25)/2=1.875
f:平方校驗：1.875*1.875=3.515625<5,得到當前下限1.875

每次得到當前值和 5 進行比較，並且記下下下限和上限，依次迭代，逐漸逼近平方根：

當結果校驗超過原值，繼續迭代
當結構校驗低於原值，獲得另一半，繼續迭代

python 代碼

import math
from math import sqrt

def sqrt_binary(num):
    x = sqrt(num)
    y = num/2.0
    low = 0.0
    up = num*1.0
    count = 1
    while abs(y-x)>0.000001:
        print(count,y)
        count += 1
        if y*y>num :
            up = y
            y = low+(y-low)/2
        else:
            low = y
            y = up-(up-y)/2
    return y

二、使用牛頓迭代法實現開方#

從函數意義上理解：我們是要求函數 f (x)=x²，使 f (x)=num 的近似解，即 x²-num=0 的近似解。

從幾何意義上理解：我們是要求抛物線 g (x)=x²-num 與 x 軸交點（g (x)=0）最接近的點。

我們假設 g (x0)=0，即 x0 是正解，那麼我們要做的就是讓近似解 x 不斷逼近 x0，這是函數導數的定義：

可以由此得到

從幾何圖形上看，因為導數是切線，通過不斷迭代，導數與 x 軸的交點會不斷逼近 x0。

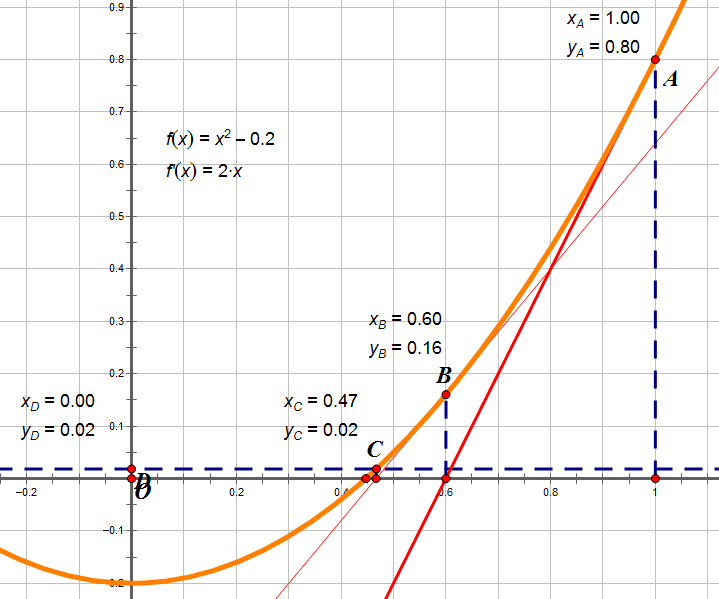
對於一般情況：

將 m=2 代入：

def sqrt_newton(num): 
  x=sqrt(num) 
  y=num/2.0 
  count=1 
  while abs(y-x)>0.00000001: 
    print count,y 
    count+=1 
    y=((y*1.0)+(1.0*num)/y)/2.0000 
  return y 
 
print(sqrt_newton(5)) 
print(sqrt(5))

三、利用牛頓迭代法實現立方#

def cube_newton(num): 
  x=num/3.0 
  y=0 
  count=1 
  while abs(x-y)>0.00000001: 
    print count,x 
    count+=1 
    y=x 
    x=(2.0/3.0)*x+(num*1.0)/(x*x*3.0) 
  return x 
 
print(cube_newton(27))