最近、ニュートン法と二分法について見ましたが、今回は Python で実装してみます。
平方根の例を取り上げます。Python プログラムで二分法とニュートン法を使って平方根を求めるコードから転載しました。
一、二分法を使って平方根を求める#
√5 を求める場合、二分法の基本的な考え方は以下の通りです。
a:半分にする: 5/2=2.5
b:平方根を確認する: 2.5*2.5=6.25>5であり、現在の上限は2.5です
c:再度半分にする: 2.5/2=1.25
d:平方根を確認する:1.25*1.25=1.5625<5であり、現在の下限は1.25です
e:再度半分にする:2.5-(2.5-1.25)/2=1.875
f:平方根を確認する:1.875*1.875=3.515625<5であり、現在の下限は1.875です
各ステップで現在の値と 5 を比較し、下限と上限を記録しながら、反復的に平方根に近づいていきます。
- 結果の確認が元の値を超える場合、続けて反復します
- 結果の確認が元の値を下回る場合、もう半分を取得し、続けて反復します
Python コード
import math
from math import sqrt
def sqrt_binary(num):
x = sqrt(num)
y = num/2.0
low = 0.0
up = num*1.0
count = 1
while abs(y-x)>0.000001:
print(count,y)
count += 1
if y*y>num :
up = y
y = low+(y-low)/2
else:
low = y
y = up-(up-y)/2
return y
二、ニュートン法を使って平方根を求める#
関数 f (x)=x² に対して、f (x)=num の近似解を求める必要があります。つまり、x²-num=0 の近似解です。
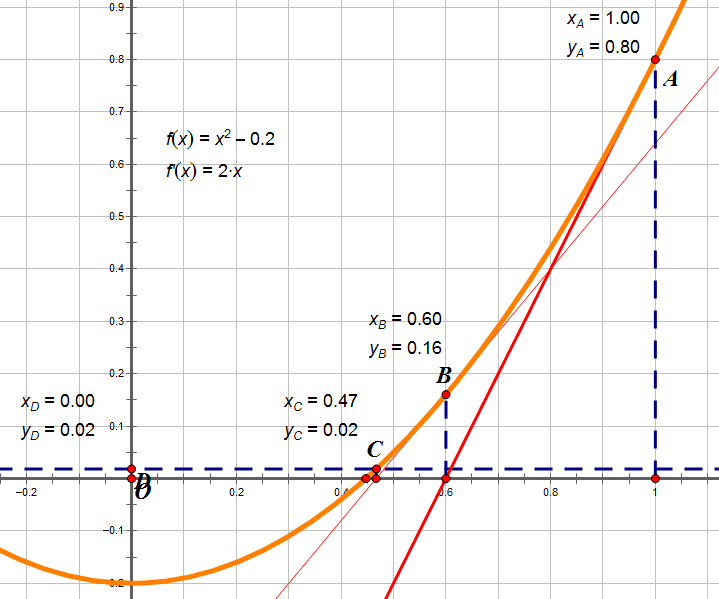
幾何学的には、抛物線 g (x)=x²-num と x 軸の交点(g (x)=0)に最も近い点を求める必要があります。
g (x0)=0 と仮定すると、x0 が正しい解であるとします。その場合、近似解 x を x0 に近づける必要があります。これは、関数の導関数の定義です:

これにより、

幾何学的に見ると、導関数は接線であり、反復的に行うことで、導関数と x 軸の交点が x0 に近づいていきます。
一般的な場合:

m=2 を代入すると:

def sqrt_newton(num):
x=sqrt(num)
y=num/2.0
count=1
while abs(y-x)>0.00000001:
print count,y
count+=1
y=((y*1.0)+(1.0*num)/y)/2.0000
return y
print(sqrt_newton(5))
print(sqrt(5))
三、ニュートン法を使って立方を求める#
def cube_newton(num):
x=num/3.0
y=0
count=1
while abs(x-y)>0.00000001:
print count,x
count+=1
y=x
x=(2.0/3.0)*x+(num*1.0)/(x*x*3.0)
return x
print(cube_newton(27))