Implementation of Newton's method iteration in Python

Recently, I came across Newton's iteration method and binary search. Now let's implement them using Python.

Taking square root as an example, reprinted from Python Programming Implementation of Binary Search and Newton's Iteration Method for Finding Square Root Code

I. Implementing Square Root using Binary Search#

Assuming we want to find the square root of 5, the basic idea of binary search is as follows:

a: Divide in half: 5/2=2.5
b: Square check: 2.5*2.5=6.25>5, and we obtain the current upper limit of 2.5
c: Divide in half again: 2.5/2=1.25
d: Square check: 1.25*1.25=1.5625<5, and we obtain the current lower limit of 1.25
e: Divide again: 2.5-(2.5-1.25)/2=1.875
f: Square check: 1.875*1.875=3.515625<5, and we obtain the current lower limit of 1.875

Compare the current value with 5 each time, and record the lower and upper limits, iterate step by step, gradually approaching the square root:

If the result exceeds the original value, continue iterating.
If the result is lower than the original value, obtain the other half and continue iterating.

Python code:

import math
from math import sqrt

def sqrt_binary(num):
    x = sqrt(num)
    y = num/2.0
    low = 0.0
    up = num*1.0
    count = 1
    while abs(y-x)>0.000001:
        print(count,y)
        count += 1
        if y*y>num :
            up = y
            y = low+(y-low)/2
        else:
            low = y
            y = up-(up-y)/2
    return y

II. Implementing Square Root using Newton's Iteration Method#

From a functional perspective: we want to find the approximate solution of the equation f(x)=x², where f(x)=num.

From a geometric perspective: we want to find the point on the parabola g(x)=x²-num that is closest to the x-axis (g(x)=0).

Let's assume g(x0)=0, where x0 is the positive solution. Our goal is to make the approximate solution x approach x0 continuously. This is the definition of the derivative:

From this, we can derive:

From a geometric perspective, because the derivative is the tangent line, through continuous iteration, the intersection of the derivative and the x-axis will approach x0.

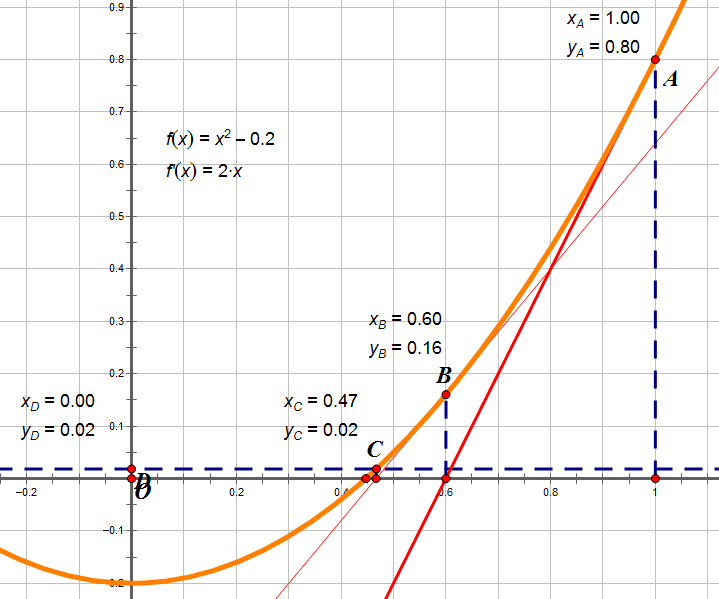
For the general case:

Substituting m=2:

def sqrt_newton(num): 
  x=sqrt(num) 
  y=num/2.0 
  count=1 
  while abs(y-x)>0.00000001: 
    print count,y 
    count+=1 
    y=((y*1.0)+(1.0*num)/y)/2.0000 
  return y 
 
print(sqrt_newton(5)) 
print(sqrt(5))

III. Implementing Cube using Newton's Iteration Method#

def cube_newton(num): 
  x=num/3.0 
  y=0 
  count=1 
  while abs(x-y)>0.00000001: 
    print count,x 
    count+=1 
    y=x 
    x=(2.0/3.0)*x+(num*1.0)/(x*x*3.0) 
  return x 
 
print(cube_newton(27))